진응력 (True Stress) 및 진변형률 (True Strain) 계산

아래 그림의 응력-변형률 곡선 (Stress-Strain Curve)은 재료의 시편에 가한 하중과 변형을 측정하여 얻은 그래프이다.

 

그림 1. Stress-Strain Curve

 

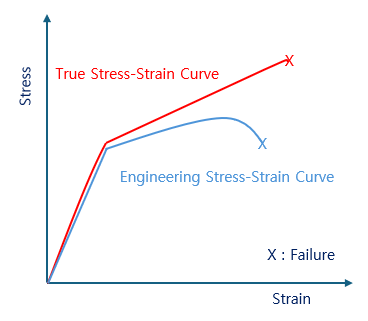
일반적으로 공학에서는 재료 시편의 최초 단면적을 기준으로 계산한 공칭응력 (엔지니어링 응력, S)과 공칭변형률 (엔지니어링 변형률, e)를 사용한다.

그러나, ABAQUS 및 ANSYS와 같은 CAE 도구로 재료의 소성 거동을 계산하기 위해서는 재료의 진응력(σ)/진변형률(ε) 데이터를 필요로 한다. 그러므로, 시험 중 계속 변하는 실제 단면적을 기준으로 진응력/진변형률 값을 계산하여 사용하기도 한다.

 

진응력이 정확한 의미의 응력이고, 변형이 커질수록 두 값의 차이도 커진다.

진응력/진변형률과 엔지니어링 응력/엔지니어링 변형률 간의 차이는 항복점 이후의 변형률 값이 더 높은 경우에는 차이가 분명하나, 탄성 영역의 경우 차이는 무시할 수 있을 정도이다.

 

아래 식을 사용하여 엔지니어링 응력/엔지니어링 변형률 값을 진응력/진변형률 값으로 변환 할 수 있다.

 

(식 1) 진응력, σ = S(1+e)

(식 2) 진변형률, ε = ln(1+e)

 

여기서,

S : Engineering Stress

e : Engineering Strain

이다.

 

Engineering Strain, e :

Engineering Stress, S :

     

True Strain, ε :

True Stress, σ :