푸아죄유 (Poiseuille’s Law)의 법칙 및 유량 계산

푸아죄유 (Poiseuille’s Law)의 법칙은 원통형 튜브를 통과하는 유체의 체적 유량 Q 와 튜브 끝단 사이의 압력 저하 ΔP 에 관한 방정식이다.

 

그림 1. 압력 저하 및 유체 흐름

 

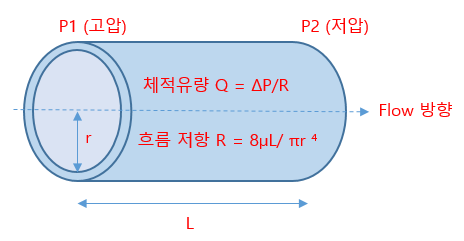
비압축 유체 층류의 경우 체적 유량은 압력 차이를 점성 저항으로 나눈 값이며, 이 저항은 점도와 길이에 선형적으로 비례하지만 반경의 4승에 반비례한다. 상당한 난류가 없는 경우, 뉴턴 유체에 대한 실험과 일치하는 것으로 증명되었다.

 

Poiseuille 의 법칙 공식 은 다음과 같다. 

 

(식 1) Q = π r ⁴ (P1 – P2) / 8μL

 

여기서,

Q : 체적유량 (m³/s)

P1과 P2 : 파이프 양단의 압력 (Pa)

r : 파이프의 반경 (m)

μ : 유체의 점도 (Pa-s)

L : 파이프의 길이 (m)

R = 8μL/πr ⁴, 유동 저항

이다.

 

유체는 항상 고압에서 저압으로 흐르며, 이 때 압력 저하 ΔP = P1 (고압) - P2 (저압)  이다. 

 

* 1 Pa-s = 1 N-s/m²

 

유체의 점도, μ (Pa-s) :

높은 압력, P1 (Pa) :

납은 압력, P2 (Pa) :

파이프의 반경, r (m) :

파이프의 길이, L (m) :

     

유동 저항, R (Pa-s/m3) :

체적 유량, Q (m3/s) :

 

예를 들어, 반경이 3 m이고 길이가 8 m인 튜브를 통해 액체가 흐릅니다. 액체의 체적 유량이 10 m³/s 일 때 튜브 끝 부분의 압력저하를 구하시오. 액체의 점도는 0.056 Pa-s 이다.

Q = πr ⁴ (P1 – P2) / 8μL 로부터, ΔP = P1 – P2 = Q * 8μL / πr ⁴  = 10 * (8*0.056*8) / (3.14*3 ⁴) = 0.14 Pa 이다.