설문조사에 적합한 표본 크기를 결정하여야 하는 변수는 모집단 규모(Population Size), 오차한계(Margin of Error), 신뢰수준(Confidence Level), 표준편차(standard deviation) 이다.
일반적으로 모집단이 클수록 정확한 결과를 생성하려면 더 큰 표본이 필요합니다.
오차한계는 결과에서 허용할 수 있는 잠재적인 변동 수준으로 오차한계가 낮을수록 더 높은 표본 크기가 필요하다. 예를 들어, 5% 오차한계를 지정하면 설문조사 응답의 95%가 실제 모집단 값의 5% 내에 속해야 합니다.
신뢰수준은 표본 크기가 대상 모집단을 정확하게 나타낼 확률이며, 설문조사 결과에 대해 얼마나 확신하는지를 나타내는 척도이다. 신뢰수준이 높을수록 데이터가 더 정확하다.
표준편차는 개별 데이터가 평균값에서 얼마나 멀리 떨어져 있는지를 설명하는 통계적 척도이다. 이 값은 실제 조사에서는 계산하기 어렵기 때문에 최악의 시나리오 비율인 0.5(50%)를 선택한다.
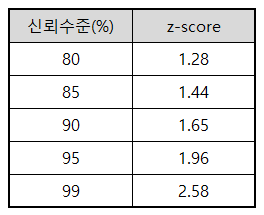
z-점수(z-score)는 개별 데이터가 평균값에서 표준편차의 몇 배만큼 떨어져 있는지 나타내는 통계적 척도이다. z-점수가 높을수록 표본 크기가 대상 모집단을 더 정확하게 나타낸다. 신뢰수준에서 구한 z-점수는 아래 표와 같다.
모집단 규모가 결정되지 않거나 무제한인 경우 아래 공식을 사용하여 샘플 크기를 계산한다.
(식 1) Sample 크기, S = Z2 * P * (1-P) / E2
더 작은 모집단에 대한 표본 크기를 식별하려는 경우 위 공식을 아래와 같이 수정할 수 있다.
(식 2) S = S / [ 1+ (S-1)/N ]
여기서,
Z : z-점수
P : 표준편차
E : 오차한계 (%)
N : 모집단 크기
이다.
위의 계산은 (식 2)를 통해 계산한 값이다. 표준편차는 최악의 시나리오 비율인 0.5(50%)를 적용하였다.
'공학 과학기술 계산 > 수학 통계' 카테고리의 다른 글
| 타원 둘레와 면적 (Perimeter & Area of Ellipse) 계산 (0) | 2024.02.26 |
|---|---|
| 나선(Helix) 길이 계산 (0) | 2024.01.26 |
| 삼각형의 3변을 통한 면적 계산 (Heron’s Formula, 헤론의 공식) (0) | 2023.12.26 |
| 호(arc)의 길이와 면적 계산 (1) | 2023.12.26 |
| 원뿔(cone) 부피, 표면적 및 중량 계산 (0) | 2023.12.24 |



